Contoh Soal Menghitung Arus pada Rangkaian Pararel Resistor
Contoh soal dan jawaban menghitung arus pada rangkaian pararel resistor. Diketahui rangkaian pararel resistor seperti gambar dibawah ini, yang terdiri dari:
R1 = 10 Ω
R2 = 20 Ω
R3 = 5 Ω
E = 12 V

Hitung berapa nilai Rtotal (Rt), Itotal (It), dan arus pada tiap-tiap resistor?
Penyelesaian:
Kita ketahui dalam rangkaian pararel seperti yang pernah ditulis dalam posting Perhitungan Rangkaian Pararel, bahwa
Rt = R1 || R2 || R3
Rt = (R1 x R2 x R3) ÷ [(R1 x R2) + (R1 x R3) + (R2 x R3)]
It = Et ÷ Rt
Et = E1 = E2 = E3
menghasilkan
I1 = E1 ÷ R1 <=> I1 = Et ÷ R1
I2 = E2 ÷ R2 <=> I2 = Et ÷ R2
I3 = E3 ÷ R3 <=> I3 = Et ÷ R3
maka diperoleh
R1 = 10 Ω
R2 = 20 Ω
R3 = 5 Ω
E = 12 V

Hitung berapa nilai Rtotal (Rt), Itotal (It), dan arus pada tiap-tiap resistor?
Penyelesaian:
Kita ketahui dalam rangkaian pararel seperti yang pernah ditulis dalam posting Perhitungan Rangkaian Pararel, bahwa
Rt = R1 || R2 || R3
Rt = (R1 x R2 x R3) ÷ [(R1 x R2) + (R1 x R3) + (R2 x R3)]
It = Et ÷ Rt
Et = E1 = E2 = E3
menghasilkan
I1 = E1 ÷ R1 <=> I1 = Et ÷ R1
I2 = E2 ÷ R2 <=> I2 = Et ÷ R2
I3 = E3 ÷ R3 <=> I3 = Et ÷ R3
maka diperoleh
- Rt = (R1 x R2 x R3) ÷ [(R1 x R2) + (R1 x R3) + (R2 x R3)]
Rt = (10 x 20 x 5) ÷ [(10 x 20) + (10 x 5) + (20 x 5)] = 2,86 Ω - It = Et ÷ Rt = 12 V ÷ 2,86 Ω = 4,2 A
- I1 = Et ÷ R1= 12 V ÷ 10 Ω = 1,2 A
- I2 = Et ÷ R2 = 12 V ÷ 20 Ω = 0,6 A
- I3 = Et ÷ R3 = 12 V ÷ 5 Ω = 2,4 A















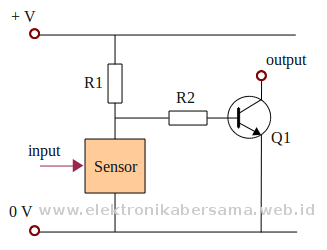
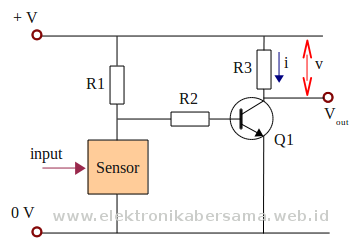


 Sensor medan magnet atau sensor efek hall dirancang untuk memberikan tanggapan terhadap intensitas medan magnet yang ada di sekitarnya.
Sensor medan magnet atau sensor efek hall dirancang untuk memberikan tanggapan terhadap intensitas medan magnet yang ada di sekitarnya. 







